Computing logarithms and roots in MATLAB

MATLAB: The Language of Technical Computing

Welcome! 

In today's post, we will be finding logarithms, both natural logarithms and logarithms to an arbitrary base. Also we would be finding roots of numbers; square roots, cube roots and eventually nth roots, where n can be any integer.

Hence lets get started!

Logarithms

I really do not think anyone would be coming to read this article without having the prior knowledge of logarithms. Understanding logarithms is fairly simple, but the sheer fact that logarithms are implemented in scientific fields so diverse and numerous makes knowing their implementations important. For the people who need only the very precise terms, here it is for them:

In mathematics, the logarithm of a number is the exponent to which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 10 to the power 3 is 1000: 1000 = 10 × 10 × 10 = 103.

 In MATLAB, both natural logarithms and logarithms to an arbitrary base can be implemented. Let us see the example below where we implement the natural logarithm and common logarithm.

Implementing Natural and Common Logarithm

Here as we can see, we use the command

y=log(x);

which results us with the natural logarithm of x.

Further we use the command

y=log10(x);

which results us with the common logarithm of x.
We can put any number after log to find the logarithm with that as a base. In the above example we just did that; found logarithm to the base 10. The 10 we put there, can be replaced with any integer we want as the base. This is called finding logarithm to an arbitrary base.

Roots of a number

To start with, as you already would have experienced growing up, finding the roots of a number is considered just that basic that it is almost a pre requisite to almost everything we do in mathematics. And surely if you've come here to read that, I do not need to stress the importance of this operation any more. Still, for the precise terms needed, lets have a basic definition here

In mathematics, a square root of a number a is a number y such that y2 = a, in other words, a number y whose square (the result of multiplying the number by itself, or y × y) is a. For example, 4 and −4 are square roots of 16 because 42 = (−4)2 = 16.

Hence moving on with the topic, let us first learn how to find square roots of numbers in MATLAB.

Square Root

Square Root is found in MATLAB using the following command:

y=sqrt(x);

where y stores the square of a number x.

The following example would help us understand better:

Finding the Square Root of a number

nth Root

To find the nth root of a number, such as the cube root or even more advanced roots of a number, you need to use a different function. The function's name is just the same as the name of this topic. Let us see a basic syntactical statement for the same:

y=nthroot(x, n);

where y stores the value of the root obtained when x is operated to 'n'th root.

Lets see an example of the same:

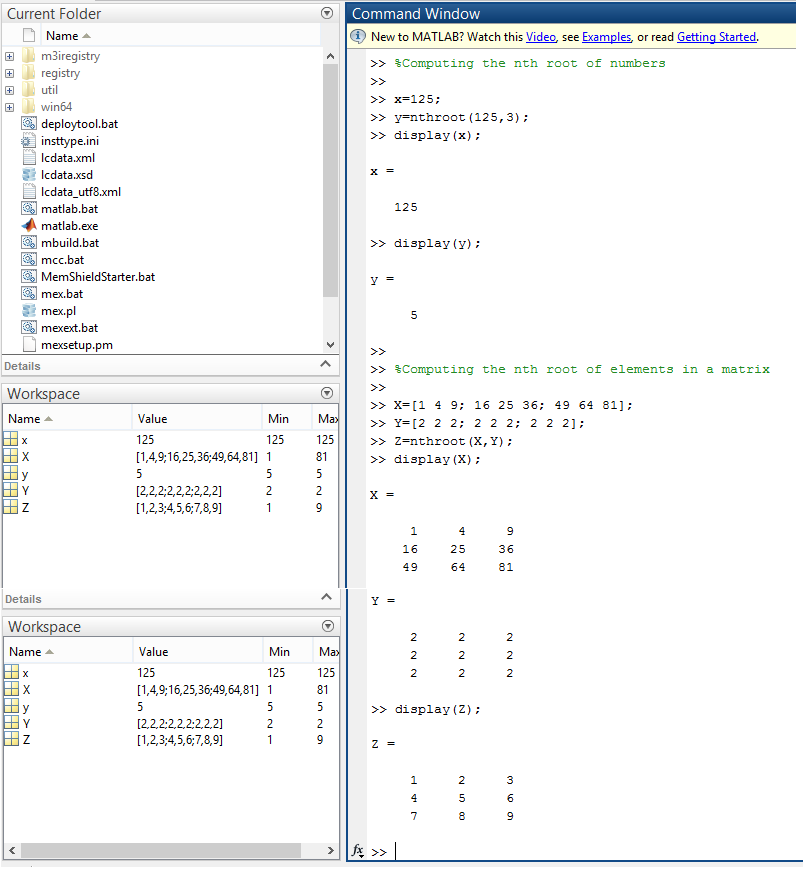Using the nthroot function in MATLAB

In the first half of the code snippet, you can see that we used the nthroot function to find the cube root of the number 125, which was correctly shown as 5.
Further we then showed the function's operability on matrices too, constructing a matrix with squares and finding their square roots with the help of another matrix containing 2 at all places. The resultant matrix hence contained the square roots of all the elements in the first matrix.

And that would hence be all that can be covered in this lesson. I hope you learned something out of it! Stay tuned for my next post. You comment for any queries always, in the space below. Till then, take care :)