Graphic Design | Digital Differential Analyzer (DDA) Algorithm

Heyo everyone! How're you doing?

Today we are going to understand a very basic algorithm in Computer Graphics, The DDA or Digital Differential Analyzer Algorithm.

Now before we get started, we should get an understanding about what DDA is and also rather what an algorithm is.

Now DDA is a line drawing algorithm. From all I can say right now, DDA is a basic algorithm used to print lines on your standard output ie. the monitor using, well, the starting point and the ending point of the lines, the starting and ending coordinate of the line that you are going to plot.



It is important to understand that the output device is basically seen as a coordinate system, hence we will be dealing with the line coordinates to have it plotted on the screen.
Let us visualise it here:

Visualising a coordinate system on our computer monitor

Also, we should begin with a basic understanding of what an algorithm is. An algorithm is basically a series of steps, a sequence of well defined steps.

So bringing it all together, the DDA Algorithm is a series of well defined steps to draw a line given we have the end points of the line, on our standard output device.

Hence lets get started now!

To begin with, we would need two coordinates; The starting and ending coordinates of the line we would wish to plot. Suppose we assume the

• starting coordinates of the line as (x1, y1)
• ending coordinates of the line as (x2, y2)

With the availability of the starting and ending points of the line we would wish to plot, we already have achieved the first step of the algorithm!

Now the second step is a manipulation of the first step. Use the starting and ending points of the line we are given to calculate the slope of the line using the following formula you might have learnt in school:

Now this algorithm takes different approaches from here depending upon if the 

• slope of the line we obtain is lesser than 1
• slope of the line we obtain is greater than 1

We would hence discuss them both below, consequently.

For lines with slope less than 1 (m<1)

Suppose we take the line as shown below:

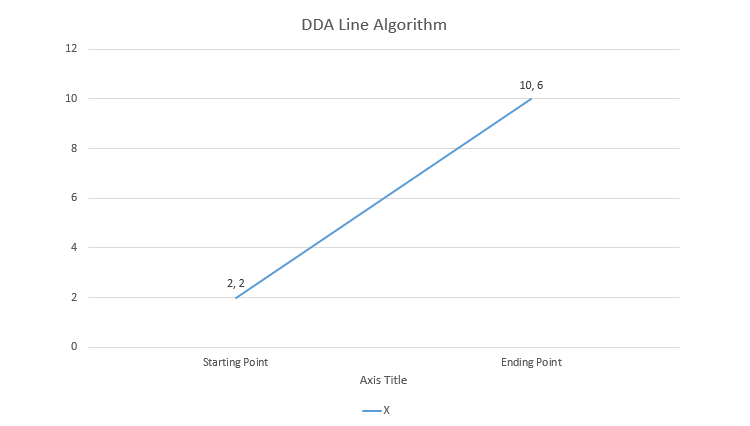DDA Algorithm for lines with slope less than 1

Using the formula for finding the slope we gave above, we can see that the slope for this line comes out to be smaller than 1 (0.5). Hence with that we now have

• The starting (2, 2) and ending (10, 6) points of the line..
• The slope (0.5) of the line.

Now comes the third step in our algorithm. Using the equation of a straight line, 

we can proceed further in our algorithm.

One thing we need to understand before we proceed further is that in computer graphics and graphic design, the role of a pixel. A pixel or a picture element is the smallest unit of a display unit that can be illuminated so as to produce an image. Hundreds and more of them combine together to form a picture on the screen. Hence we would naturally want to employ the maximum number of pixels that we can, so that we can produce the richest images possible. 

We can take the following analogy. Suppose we need to place 5 balls in a distance of 1 metre, uniformly separated from each other. Each of the balls would hence be placed at a distance of 200 centimetres from each other. Suppose we now increase the number of balls from 5 to 10. Now each ball would be placed at a distance of 100 centimetres. The line of balls, arranged together would now look more continuous than it earlier did with the individual balls placed 200 centimetres away from each other. This line would continue to appear more and more continuous as we keep increasing the balls placed. Assuming the balls to be pixels, we can similarly say that more the pixels used in creating an image, the clearer and more defined the image looks. Hence in Computer Graphics/ Graphic Design, it is always a better practise to employ the most pixels possible.

To connect it with the line we have here, if we see

• We cover 8 units going from (2,2) to (10, 6) in the X Direction
• We cover 4 units going from (2, 2) to (10, 6) in the Y Direction

Also, as we are using the coordinate system, we can only make unit increments in either direction.

And again, using the equation of the line above, we can clearly see, for a given value of X we can find a corresponding value of Y and vice versa.

Obviously hence, we would like making uniform increments along the X axis and calculating the corresponding Y axis coordinates as that would give us more number of pixels (8) than making uniform increments along the Y axis and calculating corresponding values of X axis.

Hence following up:

From

We have

Since change is x is equal to 1 and we would like to calculate corresponding values of y, we arrive at

Hence we can obtain the pixel coordinates now, starting from (x1, y1) and incrementing their values with unit increments in x direction and corresponding 'm' increments in y direction.

The following table is obtained subsequently

Pixel Coordinates

Hence we now have the coordinates we need to plot our points and to hence generate a line. The plot we so obtain is as below.

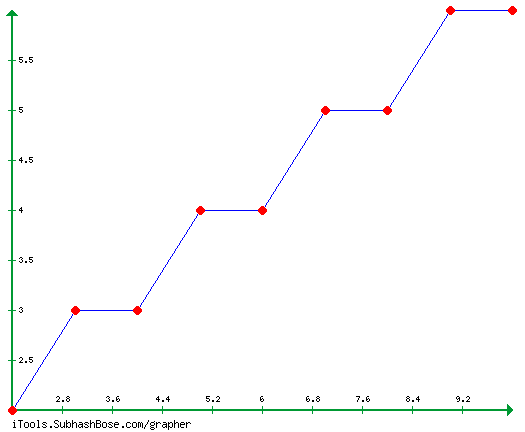The line obtained after using the DDA Line Algorithm

Now if you'd compare it with the initial example of the line we saw, this is a discontinuous line segment, breaking off, then rising up, again breaking off and leveling and then again rising and so on. This effect is called aliasing and creates jagged lines. Gamers would relate to this concept really well as all of the games nowadays feature an enhancement called Anti Aliasing or AA to resolve such graphical anomalies bound to occur due to the respective algorithms used. This effect can be reduced using more advanced (and complex) algorithms.

Moving on, let us now see the case for lines with slope > 1.

For lines with slope greater than 1 (m>1)

The very same approach would be used this time, as used last time with slopes < 1. Only this time, as you'd find, we would traverse along the Y Axis in unit increments and calculate the respective X Axis coordinates as that approach would yield more pixels this time.
For example for the line with the end points (2,10) and (5, 5)

• We cover 3 units going from (2, 10) to (5, 5) in the X Direction
• We cover 5 units going from (2, 10) to (5, 5) in the Y Direction

Also just as before

• The first step would be to have the starting and ending coordinates of the line, which we have as (2, 10) and (5, 5)
• The second step would be to find the slope of the line, using the equation

which would come out as negative (-5/3).

• The third step would ask us to calculate the value of  keeping value of  as 1 (as we make unit increments in Y Axis this time) and putting its value in the equation 
  
• This would bring the value of 
  

And just as we did above, we can plot the points, calculating at each step the value of  for each unit increment we do in Y Axis.

Now as you'd take notice, this is a topic for Computer Graphics while all we dealt with above was theory, words and equations. Here comes the coding part! The following code is written in C Language. It will help you to plot a line in a C Compiler which supports the old BGI Graphics Driver as it uses graphics.h. Using Turbo might be an alternative here. Anyways, even for educational purposes, here is the code.

#include <stdio.h>
#include <conio.h>
#include <graphics.h>
void main()
{
 int gd, gm;
 float x, y, x1, x2, y1, y2, slope;
 clrscr();
 printf("%s", "Please enter x1: ");
 scanf("%f", &x1);
 printf("%s", "Please enter y1: ");
 scanf("%f", &y1);
 printf("%s", "Please enter x2: ");
 scanf("%f", &x2);
 printf("%s", "Please enter y2: ");
 scanf("%f", &y2);
 slope=(y2-y1)/(x2-x1);
 gd=DETECT, gm;
 initgraph(&gd, &gm, "C:\\TC\\BGI");
 if(slope < 1)
 {
  for(; x1 < = x2; x1++)
  {
   y1+=slope;
   putpixel(x1, y1, RED);
  }
 }
 else
 {
  for(; y1 < = y2; y1++)
  {
   x1+=slope;
   putpixel(x1, y1, RED);
  }
 }
 getch();
 closegraph();
}

With the code and theory both understood and practised, I sign off for today, hoping to see you later in advanced Graphics topics we are going to see next. You may look here for the references for this post. Take care :)